1. 부분집합 - power set
공집합일 때 부터 1,2,3의 조합이 모두 들어갈 때 까지 즉, 집합이 0개일 때부터 1개일 때 2개일 때... 전체 다 들어갔을 때를 따져 준다.
package arr;
import java.util.Scanner;
/**
* 부분집합
*
*
* */
public class PowerSet {
static int[] arr = {1,2,3};
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
sel=new int[N];
powerset(0);
}
static public void powerset(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
if(sel[i]!=0)System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
sel[depth]=arr[depth];
powerset(depth+1);
sel[depth]=0;
powerset(depth+1);
}
}
[결과]

3 밑에 공집합인 경우인 공백도 나온다.
결과를 보면 알겠지만, 부분집합(power set)은 순서를 중요하게 생각하지 않는다.
즉, (1,2)와 (2,1)은 같은 것으로 보고 결과로 도출되지 않는다.
2. 조합 - combination
조합은 부분 집합에서 집합의 갯수를 정해놓은 셈이다.
package arr;
import java.util.Scanner;
/**
* 조합
*
*
* */
public class Combination {
static int[] arr = {1,2,3};
static int[] sel;
static int N,C;
public static void main(String[] args) {
N = 3;
C=2;
sel=new int[C];
powerset(0,0);
}
static public void powerset(int depth, int idx) {
if(depth==C) {
for(int i=0;i<C;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
if(idx == N) return;
sel[depth]=arr[idx];
powerset(depth+1,idx+1);//idx를 넘겨주면 중복 조합
sel[depth]=0;
powerset(depth,idx+1);
}
}
[결과]

결과를 보면 부분집합에서 2가지를 고려한 경우만 답으로 나오는 것을 확인할 수 있다.
즉, 전체 경우의 수를 고려해야 할 때는 부분 집합, 특정한 갯수를 꼭 채워서 고려해야한다면 조합을 사용해야 한다.
3. 순열 - permutation
부분집합과 조합과는 다르게 순서를 중요하게 생각한다. 즉, (1,2)와 (2,1)은 다른 것으로 보고 결과로 도출한다.
package arr;
import java.util.Scanner;
/**
* 순열
* 순서 전체를 돌려줘야함
* 선택된 곳은 가면 안됨 -> 같은 숫자가 나오는 경우는 없음
* */
public class Permutation {
static int[] arr = {1,2,3};
static boolean[] visited;
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
visited = new boolean[N];
sel=new int[N];
permutation(0);
}
static public void permutation(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
for(int i=0;i<N;i++) {
if(visited[i]) continue;
sel[depth]=arr[i];
visited[i]=true;
permutation(depth+1);
visited[i]=false;
}
}
}
[결과]
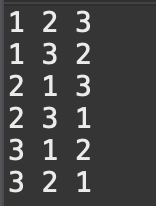
4. next permutation
사전 순으로 순열의 결과를 출력해준다. 이 때 중복되는 숫자가 있어도 동일한 경우의 수는 출력되지 않는다.
package arr;
import java.util.Arrays;
public class NextPermutation {
static int[] arr= {1,2,3};
public static void main(String[] args) {
Arrays.sort(arr);
do {
System.out.println(Arrays.toString(arr));
}while(nextPermutation());
}
static public boolean nextPermutation() {
int N = arr.length;
int idx_a = N-1;
while(idx_a>0 && arr[idx_a-1]>=arr[idx_a]) idx_a--;
if(idx_a==0) return false;
int idx_b = N-1;
while(arr[idx_a-1]>=arr[idx_b]) idx_b--;
swap(idx_a-1,idx_b);
int k = N-1;
while(idx_a<k) {
swap(idx_a++,k--);
}
return true;
}
static public void swap(int idx_a, int idx_b) {
int temp = arr[idx_a];
arr[idx_a]=arr[idx_b];
arr[idx_b]=temp;
}
}
[중복되지 않은 수로 이뤄진 배열의 결과]

[중복된 수로 이뤄진 배열의 결과]
ex ) 1,1,3
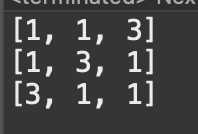
위와 비교하여 그냥 순열로 돌리면 다음과 같이 중복된 결과를 볼 수 있다. 왜냐하면 순열은 (1,2) (2,1)을 다른 경우로 보기 때문에 같은 (1,1)이어도 다른 (1,1)로 보기 때문이다.
[1,1,3을 그냥 순열로 돌렸을 때 결과]

참고로 나는 next permutation 이해가 안가서 그냥 외우고 있다...
끝
'알고리즘 > 이론' 카테고리의 다른 글
| C strtok (1) | 2023.11.03 |
|---|---|
| SWEA 미로 1 문제를 통해 알아보는 DFS / BFS (0) | 2023.04.04 |
| 이진검색 & 정렬 정리 (0) | 2023.03.27 |
| [JAVA] 카운팅 정렬 step3 완벽 이해 (0) | 2023.02.19 |
| [JAVA] 이웃한 요소와의 차의 절대값 구하기 - 델타배열 활용 (0) | 2023.02.19 |
1. 부분집합 - power set
공집합일 때 부터 1,2,3의 조합이 모두 들어갈 때 까지 즉, 집합이 0개일 때부터 1개일 때 2개일 때... 전체 다 들어갔을 때를 따져 준다.
package arr;
import java.util.Scanner;
/**
* 부분집합
*
*
* */
public class PowerSet {
static int[] arr = {1,2,3};
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
sel=new int[N];
powerset(0);
}
static public void powerset(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
if(sel[i]!=0)System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
sel[depth]=arr[depth];
powerset(depth+1);
sel[depth]=0;
powerset(depth+1);
}
}
[결과]

3 밑에 공집합인 경우인 공백도 나온다.
결과를 보면 알겠지만, 부분집합(power set)은 순서를 중요하게 생각하지 않는다.
즉, (1,2)와 (2,1)은 같은 것으로 보고 결과로 도출되지 않는다.
2. 조합 - combination
조합은 부분 집합에서 집합의 갯수를 정해놓은 셈이다.
package arr;
import java.util.Scanner;
/**
* 조합
*
*
* */
public class Combination {
static int[] arr = {1,2,3};
static int[] sel;
static int N,C;
public static void main(String[] args) {
N = 3;
C=2;
sel=new int[C];
powerset(0,0);
}
static public void powerset(int depth, int idx) {
if(depth==C) {
for(int i=0;i<C;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
if(idx == N) return;
sel[depth]=arr[idx];
powerset(depth+1,idx+1);//idx를 넘겨주면 중복 조합
sel[depth]=0;
powerset(depth,idx+1);
}
}
[결과]

결과를 보면 부분집합에서 2가지를 고려한 경우만 답으로 나오는 것을 확인할 수 있다.
즉, 전체 경우의 수를 고려해야 할 때는 부분 집합, 특정한 갯수를 꼭 채워서 고려해야한다면 조합을 사용해야 한다.
3. 순열 - permutation
부분집합과 조합과는 다르게 순서를 중요하게 생각한다. 즉, (1,2)와 (2,1)은 다른 것으로 보고 결과로 도출한다.
package arr;
import java.util.Scanner;
/**
* 순열
* 순서 전체를 돌려줘야함
* 선택된 곳은 가면 안됨 -> 같은 숫자가 나오는 경우는 없음
* */
public class Permutation {
static int[] arr = {1,2,3};
static boolean[] visited;
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
visited = new boolean[N];
sel=new int[N];
permutation(0);
}
static public void permutation(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
for(int i=0;i<N;i++) {
if(visited[i]) continue;
sel[depth]=arr[i];
visited[i]=true;
permutation(depth+1);
visited[i]=false;
}
}
}
[결과]

4. next permutation
사전 순으로 순열의 결과를 출력해준다. 이 때 중복되는 숫자가 있어도 동일한 경우의 수는 출력되지 않는다.
package arr;
import java.util.Arrays;
public class NextPermutation {
static int[] arr= {1,2,3};
public static void main(String[] args) {
Arrays.sort(arr);
do {
System.out.println(Arrays.toString(arr));
}while(nextPermutation());
}
static public boolean nextPermutation() {
int N = arr.length;
int idx_a = N-1;
while(idx_a>0 && arr[idx_a-1]>=arr[idx_a]) idx_a--;
if(idx_a==0) return false;
int idx_b = N-1;
while(arr[idx_a-1]>=arr[idx_b]) idx_b--;
swap(idx_a-1,idx_b);
int k = N-1;
while(idx_a<k) {
swap(idx_a++,k--);
}
return true;
}
static public void swap(int idx_a, int idx_b) {
int temp = arr[idx_a];
arr[idx_a]=arr[idx_b];
arr[idx_b]=temp;
}
}
[중복되지 않은 수로 이뤄진 배열의 결과]

[중복된 수로 이뤄진 배열의 결과]
ex ) 1,1,3

위와 비교하여 그냥 순열로 돌리면 다음과 같이 중복된 결과를 볼 수 있다. 왜냐하면 순열은 (1,2) (2,1)을 다른 경우로 보기 때문에 같은 (1,1)이어도 다른 (1,1)로 보기 때문이다.
[1,1,3을 그냥 순열로 돌렸을 때 결과]

참고로 나는 next permutation 이해가 안가서 그냥 외우고 있다...
끝
'알고리즘 > 이론' 카테고리의 다른 글
| C strtok (1) | 2023.11.03 |
|---|---|
| SWEA 미로 1 문제를 통해 알아보는 DFS / BFS (0) | 2023.04.04 |
| 이진검색 & 정렬 정리 (0) | 2023.03.27 |
| [JAVA] 카운팅 정렬 step3 완벽 이해 (0) | 2023.02.19 |
| [JAVA] 이웃한 요소와의 차의 절대값 구하기 - 델타배열 활용 (0) | 2023.02.19 |
