
1) 사이트
1929번: 소수 구하기
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
www.acmicpc.net
2) 문제

이번 문제 2581번 소수 문제를 풀었던 사람이라면, '아 뭐야 개 쉽다'하고 코드 변형해서 내면 <시간 초과>라는 문구를 보실 수 있습니다.
2581번 소수
1) 사이트 2581번: 소수 M이상 N이하의 자연수 중 소수인 것을 모두 찾아 첫째 줄에 그 합을, 둘째 줄에 그 중 최솟값을 출력한다. 단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출
tksgk2598.tistory.com
저도 그랬거든요...
그래서 네이버 검색 창에 <소수 알고리즘 시간복잡도>를 치니 다양하게 코드를 짤 수 있더군요.
저는 이 블로그에서 도움을 받았습니다.
JM's IT Blog
개발쟁이가 되기 위한 생초짜의 기술 블로그 기록기
jm-park.github.io
특히 아래 이미지를 보며 많은 도움을 받았는데요. 루트(검사하고 싶은 숫자) 만큼의 배수를 검사하면, 그 뒤로는 모두 소수라는 사실 입니다 : ) 16을 예를 들어볼까요? 루트(16) = 4의 배수까지만 검사하면 합성수가 얼추 걸러진다는 소리입니다.
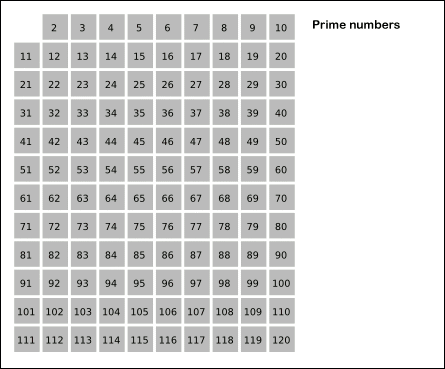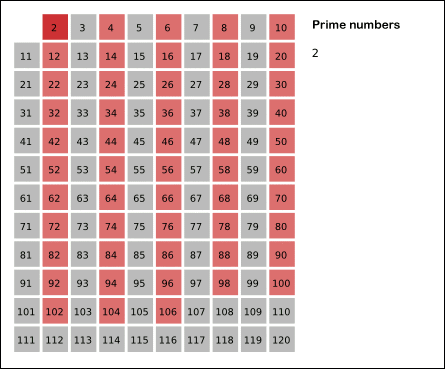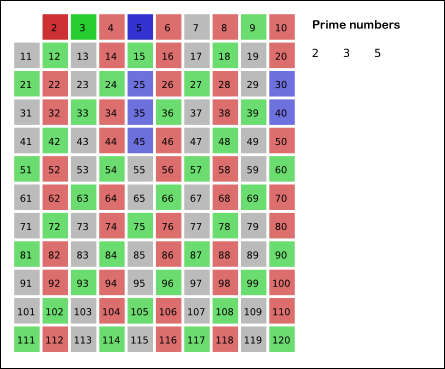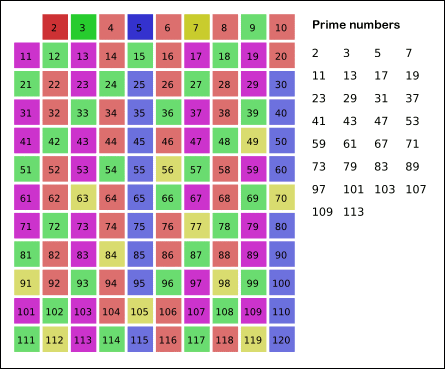
참고로 적자면, 1~100까지의 소수는 다음과 같습니다. 코드 짜시고, 테스트 해보고 싶으실 때 유용하실 것 같습니다.
1~10 : 2, 3, 5, 7
11~20 : 11, 13, 17, 19
21~30 : 23, 29
31~40 : 31, 37
41~50 : 41, 43, 47
51~60 : 53, 59
61~70 : 61, 67
71~80 : 71, 73, 79
81~90 : 83, 89
91~100 : 97
3) 파이썬 코드
import math
flag=0 #0이면 소수 1이면 합성수
min, max=map(int, input().split(' '))
for i in range(min,max+1):
#1과 짝수는 소수가 아니다. (단, 2는 짝수 중 유일한 소수)
if i==1 or (i!=2 and i%2==0) :
continue
elif int(math.sqrt(i))<4:
for j in range(2,i):
#합성수이면 다음 수 검사하게 멈춘다.
if(i%j==0):
flag=1
break
else:
#16부터 들어와야 할 것 같음
for j in range(2,int(math.sqrt(i))+1):
#합성수이면 다음 수 검사하게 멈춘다.
if(i%j==0):
flag=1
break
if flag==1:
flag=0
else:
print(i)
3-1) 선수 지식
파이썬 코드를 이해하기 위해 알아야 할 선수 지식이 있습니다.
1. sqrt, 제곱근 쓰는 방법
>import math
>math.sqrt(숫자)
3-2) 설명
1. 사용할 변수를 선언 및 초기화 해줍니다.
import math
flag=0 #0이면 소수 1이면 합성수flag는 소수인지 합성수인지 구분하게 도와줍니다.
2. 소수를 골라낼 구간을 입력 받습니다.
min, max=map(int, input().split(' '))
3. 입력 받은 구간만큼 반복문을 돌립니다.
for i in range(min,max+1):
4. 1과 짝수는 소수가 아니므로 사전에 처리합니다. 짝수 중 2는 유일한 소수이므로 주의하셔야 합니다.
for i in range(min,max+1):
#1과 짝수는 소수가 아니다. (단, 2는 짝수 중 유일한 소수)
if i==1 or (i!=2 and i%2==0) :
continue
5. 루트(검사하는 수)가 4^2=16보다 작으면 2~자신의수-1까지 나눠 떨어지는 지 검사합니다.
elif int(math.sqrt(i))<4:
for j in range(2,i):
#합성수이면 다음 수 검사하게 멈춘다.
if(i%j==0):
flag=1
break예를 들어 2~루트(9)까지 검사하면, for i in range(2,3) 즉 2~2를 조사하는 것과 같아 제대로 된 값이 도출되지 않습니다.
6. 루트(검사하는 수)가 16이상이면 2~루트(검사하는수)까지 검사해 나눠 떨어지는 지 검사합니다.
else:
#16부터 들어와야 할 것 같음
for j in range(2,int(math.sqrt(i))+1):
#합성수이면 다음 수 검사하게 멈춘다.
if(i%j==0):
flag=1
break1~100000까지 했을 때 제한 시간이 훌쩍 넘어가서, 2초가 넘어가는 숫자를 대상으로는 시간복잡도 O(루트(N))을 이용했습니다.
7. 최종적으로 flag=1이면 합성수이고 0이면 소수인 것을 결과로 출력한다.
if flag==1:
flag=0
else:
print(i)
4) c언어
없음
궁금한 점이나 공유할 정보가 있다면 댓글로 남겨주세요 *^^*
끝!
'알고리즘 > 백준' 카테고리의 다른 글
| 9020번 골드바흐의 추측 (0) | 2021.07.21 |
|---|---|
| 4948번 베르트랑 공준 (0) | 2021.07.17 |
| 11653번 소인수분해 (0) | 2021.07.16 |
| 2581번 소수 (0) | 2021.07.16 |
| 1978번 소수 찾기 (0) | 2021.07.15 |
