
2달 전에 맞췄던 문제, 또 풀어본다.
너무 오랜만에 알고리즘을 푸니... static 쓰는 것도 까먹는 나...
오늘은 오랜만에 MST 문제를 풀어보았다.
다시 개념을 살펴보자면 MST는 최소신장트리이다.
신장 트리 중에 사용된 간선들의 가중치 합이 최소인 트리이다.
도로망, 통신망, 유통망 등 비용을 최소로 해야 이익을 볼 수 있을 때 사용한다.
대표적인 방법으로 크루스칼과 프림이 있는데,
오늘의 문제는 합집합 연산을 하고, 같은 부모를 갖는지 확인해야하는 작업이었기 때문에
딱히 MST 문제는 아니지만, 크루스칼이 적격이라고 생각해서 크루스칼로 풀었다.
2달 전에 나도 크루스칼로 풀었다는 사실! ^^
1. 출처
1717번: 집합의 표현
초기에 $n+1$개의 집합 $\{0\}, \{1\}, \{2\}, \dots , \{n\}$이 있다. 여기에 합집합 연산과, 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산을 수행하려고 한다. 집합을 표현하는 프로그램을 작
www.acmicpc.net
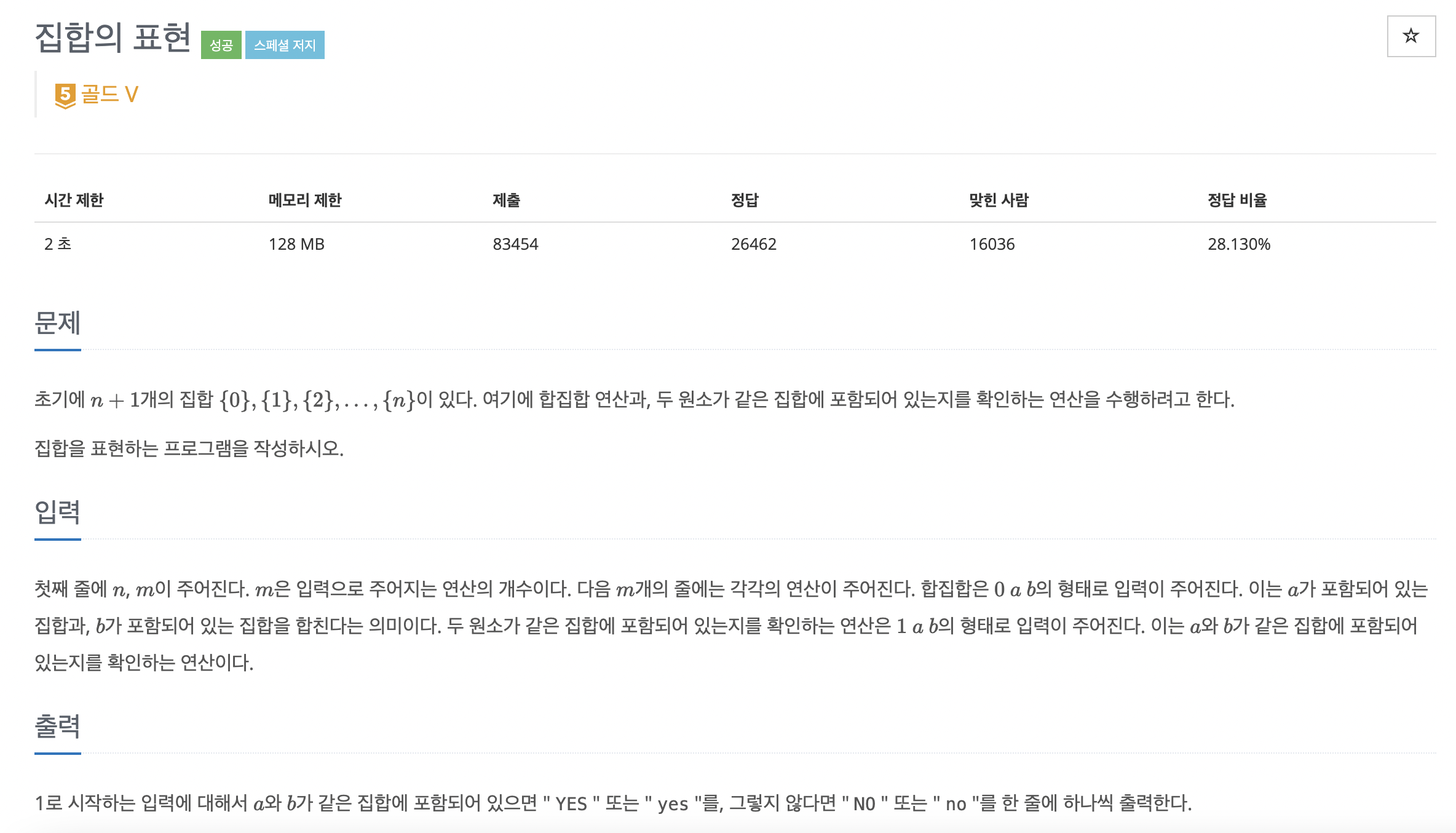

크루스칼만 떠올랐다면 어렵지 않게 풀 수 있는 문제이다.
2. 설계
같은 합집합을 가졌는지는 같은 부모를 가졌는지로 판단한다.
=> findP 함수에서 해줄 것이다.
합집합 연산은 union 함수에서 해줄 것이다.
=> union
1. 입력 값 받기
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
maxNum = sc.nextInt();
parent = new int[maxNum+1];
rank = new int[maxNum+1];
calCount = sc.nextInt();
위에 쓰인 변수들은 모두 전역변수로 static 처리를 해놓았다.
한 테스트 케이스에서 나올 수 있는 최대 숫자를 maxNum이라고 하여 만약 7이라고 하면 1~7까지의 수가 나온다는 의미이다.
parent는 각 자식은 어떤 부모를 가졌는지를 저장한다.
rank는 자식이 많은 부모를 판결하는데 사용한다.
calCount는 연산 횟수이다. 즉 테스트케이스 수이다.
2. 부모를 자기 자신으로 셋팅
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
maxNum = sc.nextInt();
parent = new int[maxNum+1];
rank = new int[maxNum+1];
calCount = sc.nextInt();
//시작 전 부모 초기 셋팅
setP();
}
//부모를 자기 자신으로 셋팅
public static void setP() {
for(int i=1;i<=maxNum;i++) {
parent[i]=i;
}
}
가장 먼저 각 자식의 부모를 자기 자신으로 셋팅하는 과정이 필요하다.
이 과정을 거치지 않으면 모든 자식은 부모를 0으로 가지고 있어 두 부모가 같은지 확인하는 모드에서 모두 "YES"가 나올 것이다.
3. 모드에 맞는 과정을 진행한다.
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
maxNum = sc.nextInt();
parent = new int[maxNum+1];
rank = new int[maxNum+1];
calCount = sc.nextInt();
//시작 전 부모 초기 셋팅
setP();
for(int T=1;T<=calCount;T++) {
int mode = sc.nextInt(); //0이면 합집합모드, 1이면 확인모드
int num1 = sc.nextInt();
int num2 = sc.nextInt();
if(mode == 0) {
//합집합 모드
if(findP(num1)==findP(num2)) continue;
union(num1, num2);
}else if(mode == 1) {
if(findP(num1)==findP(num2)) System.out.println("YES");
else System.out.println("NO");
}
}
}
//부모를 자기 자신으로 셋팅
public static void setP() {
for(int i=1;i<=maxNum;i++) {
parent[i]=i;
}
}
//자식의 부모를 찾아준다
public static int findP(int child) {
if(parent[child]==child) return child;
else return findP(parent[child]);
}
//합집합
public static void union(int c1, int c2) {
int c1_p = findP(c1);
int c2_p = findP(c2);
//둘의 부모가 다른 것만 들어온다고 가정
if(rank[c1_p]>=rank[c2_p]) {
parent[c2_p] = c1_p;
rank[c1_p]++;
}else {
parent[c1_p] = c2_p;
rank[c2_p]++;
}
}
모드가 0일 경우 합집합 모드여서 두 자식의 부모가 같은지 꼭! 확인하고, union 함수를 진행한다.
합집합 함수에서는 두 자식의 부모의 랭크 중 더 높은 랭크를 가진 부모 아래로 나머지 부모가 들어가게 한다.
그리고 자식을 하나 더 가진 부모는 랭크를 올려주면 된다.
모드가 1일 경우 같은 부모를 갖는지 확인하는 모드이다. 때문에 findP함수를 진행하고,
부모가 같으면 YES, 같지 않으면 NO를 출력하면 된다.
제한 시간은 2초이기 때문에 구지 StringBuilder를 사용해주지 않았다.
3. 전체코드
import java.util.Scanner;
public class BJ1717 {
static int maxNum;
static int[] parent;
static int[] rank;
static int calCount;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
maxNum = sc.nextInt();
parent = new int[maxNum+1];
rank = new int[maxNum+1];
calCount = sc.nextInt();
//시작 전 부모 초기 셋팅
setP();
for(int T=1;T<=calCount;T++) {
int mode = sc.nextInt(); //0이면 합집합모드, 1이면 확인모드
int num1 = sc.nextInt();
int num2 = sc.nextInt();
if(mode == 0) {
//합집합 모드
if(findP(num1)==findP(num2)) continue;
union(num1, num2);
}else if(mode == 1) {
if(findP(num1)==findP(num2)) System.out.println("YES");
else System.out.println("NO");
}
}
}
//크루스칼
//부모를 자기 자신으로 셋팅
public static void setP() {
for(int i=1;i<=maxNum;i++) {
parent[i]=i;
}
}
//자식의 부모를 찾아준다
public static int findP(int child) {
if(parent[child]==child) return child;
else return findP(parent[child]);
}
//합집합
public static void union(int c1, int c2) {
int c1_p = findP(c1);
int c2_p = findP(c2);
//둘의 부모가 다른 것만 들어온다고 가정
if(rank[c1_p]>=rank[c2_p]) {
parent[c2_p] = c1_p;
rank[c1_p]++;
}else {
parent[c1_p] = c2_p;
rank[c2_p]++;
}
}
}
최근에 토스(Toss) 코딩 테스트 문제를 풀었는데,
정말 어려웠다... 1번 문제 빼고는 다양한 테스트케이스에 걸려 진땀났다 ㅎㅎ
그래도 그렇게 어려운 문제를 치루고 나니
나는 아직 공부해야할 알고리즘 문제가 많다고 느낄 수 있었다.
현재 프로젝트 속에서 바쁘다는 핑계로 알고리즘을 놓고 살았는데,
정신이 번쩍 들었다.
'알고리즘 > 백준' 카테고리의 다른 글
| [DFS/구현] 백준 15683번 감시 - JAVA (0) | 2023.07.21 |
|---|---|
| [순열/해시맵] 백준 5568번 카드놓기 - JAVA (0) | 2023.07.17 |
| [트리] 백준 3584번 가장 가까운 공통 조상 - JAVA (0) | 2023.07.01 |
| [문자열] 백준 1593번 문자 해독 - JAVA (0) | 2023.06.25 |
| [BFS/DFS/MST] 백준 17472번 다리 만들기2 - JAVA (0) | 2023.06.23 |
