0. 인트로
나는 사실 LCS 문제를 처음 풀어본다. 그래서 혼자 풀어보려니 시간초과만 나고 답도 틀리고 잘 풀리지 않았다. 그래서 여러 LCS 설명을 찾아봤는데, 무슨 말인지 통 모르겠더란다... 그러던 찰나에 발견한 한 유튜브 강의가 내 이해를 도왔다. 영상 길이는 4분이라는 짧은 시간인데, 내 이해를 단번에 도왔다.
https://www.youtube.com/watch?v=MeE-GSikiE4
1. LCS란?
LCS는 최장 공통 부분 수열의 길이를 구하는 문제이다. 예를 들면 아래와 같은 문제이다.
9251번: LCS
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
LCS는 대표적인 DP문제이다. DP라고 하면 당연 점화식이 필요하다. 그렇다면 LCS의 점화식은 무엇일까?
1) 만약 i==0 || j==0이면 dp[i][j]는 0이다. 즉, 행과 열 모두 1부터 사용한다는 의미와 같다.
2) 만약 문자1와 문자2가 달라서 LCS에 포함되지 않는다면, dp[i][j-1]과 dp[i-1][j] 중 큰 결과값을 선택한다.
3) 만약 문자1과 문자2가 같아서 LCS에 포함이 된다면 dp[i-1][j-1]+1을 결과값으로 선택한다.
나는 수많은 블로그와 유튜브에서 이러한 점화식을 낸다는 것을 이해했지만, 어떻게 해석해야할지 난감한 상태였다.
2. LCS 점화식 해석
영상에서는 간단명료하게 LCS 점화식을 해석해주셨다.
2-1) 2번 점화식 해석
2) 만약 문자1와 문자2가 달라서 LCS에 포함되지 않는다면, dp[i][j-1]과 dp[i-1][j] 중 큰 결과값을 선택한다.
문자열 1
ACAYKP
문자열2
CAPCAK
다음 2개의 문자열에서 문자열1의 첫번째 문자 'A'와 문자열2의 첫번째 문자 'C'는 서로 달라 LCS 조건에 충족되지 않는다.
때문에 문자열1 입장에서 i번째 'A'가 LCS에 충족되지 않는다면 그 이전의 값 i-1의 값을 그대로 써야하기 때문에 dp[i-1][j] 를 이용한다.
동일한 이유로 문자열2 입장에서 j번째 'C'가 LCS에 충족되지 않는다면 그 이전의 값 j-1의 값을 그대로 써야하기 때문에 dp[i][j-1]을 이용한다.
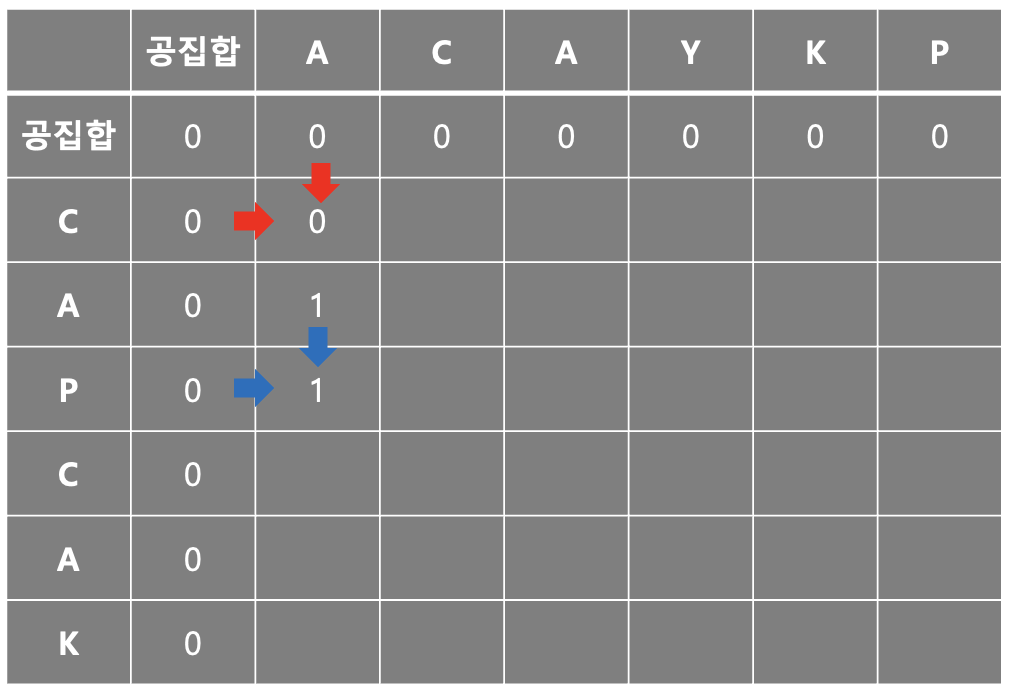
그림으로 보면 빨간색 부분 A와 C는 LCS에 포함되지 않기 때문에 A의 바로 이전의 값과 C의 바로 이전의 값 중 가장 큰 값으로 가져온다. 그래서 0이다.
한 번 더 이해를 돕기 위해 파란색 부분을 살펴보자.
파란색 부분도 A와 P가 LCS에 포함되지 않기 때문에 A의 바로 이전의 값과 P의 바로 이전의 값 중 가장 큰 값으로 가져온다. 그래서 1이다.
2-2) 3번 점화식 해석
3) 만약 문자1과 문자2가 같아서 LCS에 포함이 된다면 dp[i-1][j-1]+1을 결과값으로 선택한다.
2-1번은 이해했다면 이 해석은 쉽다. 문자열1의 i위치와 문자열2의 j위치의 문자가 LCS에 포함된다면 1~i-1 위치까지 계산한 결과와 1~j-1위치까지 계산한 결과 즉, 바로 이전 계산 결과에 +1을 더해주면 되는 것이다.
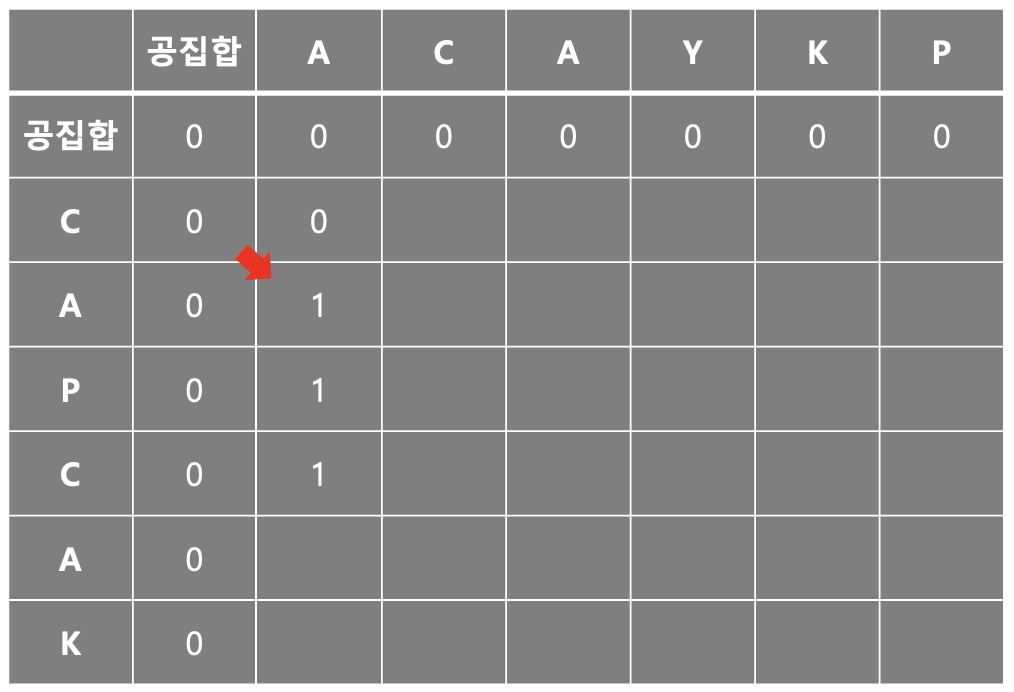
i-1 j-1은 대각선위치이기 때문에 LCS에 포함되는 문자의 경우 대각선 위치 값에서 +1을 그래서 가져오는 것이다.
이 원리를 알기 이전에 나는 그다음에 A가 또 나오면 어떻게 되는거지? 라는 의문이 있었다. 2가되면 안되는데 어떻게 예외를 주면 좋을까? 하는 의문이었다. 하지만 왜 대각선 방향에서 +1을 해주어야하는지 확실히 이해하고, 왜 다음에 2가 나오지 않고 그대로 1이 나오는지 명확히 이해할 수 있었다!
2-3) 1번 점화식 해석
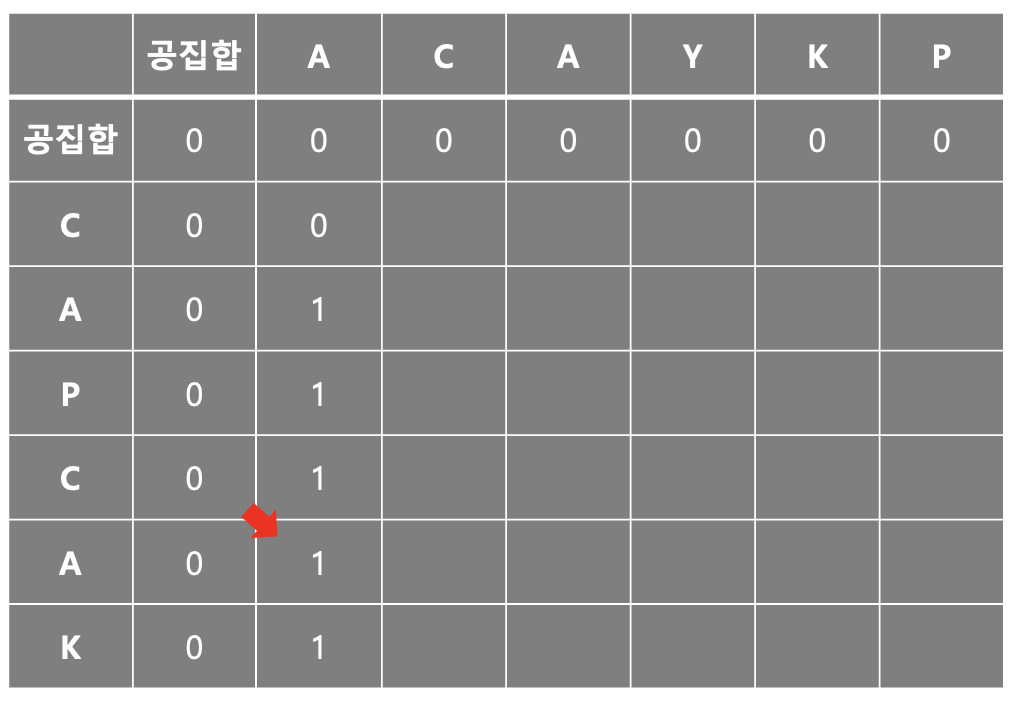
1) 만약 i==0 || j==0이면 dp[i][j]는 0이다. 즉, 행과 열 모두 1부터 사용한다는 의미와 같다.
2-1와 2-2의 방식을 이해했다면 원활한 계산을 위해 (1,1) 위치부터 시작하는 게 좋은 이유가 이해가 될 것이다.
만약 공집합 라인이 없었다면 -1 인덱스로 갔을 때 예외 조건을 한 번 더 써줘야 할 것이다.
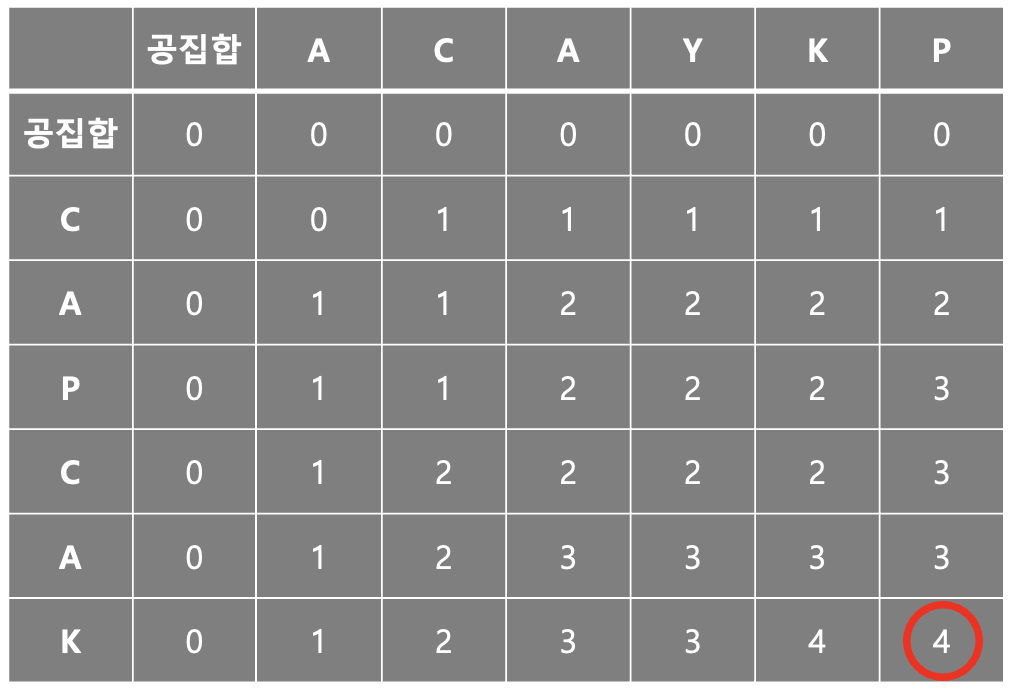
그리하여 정답은 아래와 같다.
3. LCS 코드
import java.util.*;
import java.io.*;
//0.4초
//LCS
class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String str1 = br.readLine();
String str2 = br.readLine();
int str1Len = str1.length();
int str2Len = str2.length();
int dp[][] = new int[str2Len+1][str1Len+1];
for(int i=1;i<=str1Len;i++){
for(int j=1;j<=str2Len;j++){
if(str1.charAt(i-1)==str2.charAt(j-1)){//charAt은 0부터 시작 주의
dp[j][i] = dp[j-1][i-1]+1;
}
else{
dp[j][i] = Math.max(dp[j-1][i], dp[j][i-1]);
}
}
}
System.out.println(dp[str2Len][str1Len]);
}
}
dp 인덱스는 1부터 돌지만, charAt이나 char 배열을 쓰는 경우 0부터 인덱스가 시작한다는 사실 잊지말자!
'알고리즘 > 이론' 카테고리의 다른 글
| 자바에서 정렬하기 4가지 방법 (2) | 2024.01.18 |
|---|---|
| 하노이탑 이동 공식 (0) | 2024.01.04 |
| 투포인터 (1) | 2023.11.28 |
| C strtok (1) | 2023.11.03 |
| SWEA 미로 1 문제를 통해 알아보는 DFS / BFS (0) | 2023.04.04 |
