
안녕하세요 : )
SSAFYicial 9기 신산하입니다.
벌써 하반기 시즌입니다 ㅠㅠ
자기소개서 쓰기도 바쁜데 알고리즘 공부는 언제하죠?...
저와 여러분 모두를 위해 준비했습니다.
알고리즘 총정리!
(정렬은 제외하겠습니다 ㅎㅎ)

지금부터 시작합니다!
1. 완전 검색 (Brute-force 혹은 Generate-and-Test 기법)
브루트포스 알고리즘이라고도 합니다. 무차별적으로 대입해서 푸는 것이죠. 무식해보이지만 가장 기본적인 방법이 됩니다. 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 작습니다.
예시 문제 ) 베이비 진 (16546. Baby-gin_실습)
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
여러분 베이비 진 문제 기억하시나요?
0~9 사이의 숫자 카드에서 임의의 카드 6 장을 뽑았을 때 , 3 장의 카드가 연속적인 번호를 갖는 경우를 run 이라 하고 , 3 장의 카드가 동일한 번호를 갖는 경우를 triplet 이라고 합니다. 또한 6 장의 카드가 run 과 triplet 로만 구성된 경우를 baby gin으로 불립니다.
즉, 6 자리의 숫자를 입력 받아 baby gin 여부를 판단하는 프로그램을 작성하는 문제입니다.
package test;
public class 순열버전 {
public static void main(String[] args) {
// a부터 b까지의 연속된 숫자 중에서
// 3개를 뽑아서 나열하는 순열
int a=1;
int b=3;
//1, 2, 3, 4 네 개의 숫자 중에서 3개를 뽑아 나열하는 순열
for(int i=a; i<=b; i++) {
for(int j=a; j<=b; j++) {
//j는 어떤 수만 올 수 있나요?
//j는 i가 아닌 수만 올 수 있다.
if(j != i) {
//if문 안에서 그 다음 for문이 돌아가야겠죠?
for(int k=a;k<=b;k++) {
//k는 어떤 수가 올 수 있죠?
//k는 i도 아니고 j도 아니어야 함
if(k != i && k != j) {
System.out.printf("%d %d %d\n",i,j,k);
}
}
}
}
}
}
}
이런 식으로 3개를 뽑아서 나열하는 순열로도 문제를 풀 수 있지만,
package test;
import java.util.Arrays;
public class Babygin_완전검색 {
public static void main(String[] args) {
int[] cards = {1, 1, 2, 2, 3, 3};
for(int i=0; i<6; i++) {
for(int j=0; j<6; j++) {
if(i != j) {
for(int k=0; k<6; k++) {
if(k != i && k != j) {
for(int l=0; l<6; l++) {
if(l != i && l != j && l != k) {
for(int m=0; m<6; m++) {
if(m != i && m != j && m != k && m != l) {
for(int n=0; n<6; n++) {
if(n != i && n != j && n != k && n != l && n != m) {
if(tripletOrRun(cards[i], cards[j], cards[k]) && tripletOrRun(cards[l], cards[m], cards[n])) {
System.out.println("babygin!");
return;
}
}
}
}
}
}
}
}
}
}
}
}
}
private static boolean tripletOrRun(int i, int j, int k) {
return (i == j && j == k )||(j == i + 1 && k == i+2);
}
}이런식으로 6가지 수를 완전탐색하는 경우 6개의 for문을 써주면 됩니다.
엄청난 악어새의 크기를 볼 수 있죠 : )
2. 탐욕 알고리즘 (Greedy Algorithm)
탐욕 알고리즘은 최적해를 구하는 데 사용되는 근시안적인 방법입니다. 여기서 최적해는 최소값, 최대값을 말합니다. 최소값과 최대값은 1개입니다.
또한 탐욕알고리즘의 맹점은 각 선택의 시점에서 이루어지는 결정은 지역적(local)으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 하여 그것이 최적이라는 보장은 없다는 것입니다.
예시 문제 ) 거스름돈 (1970. 쉬운 거스름돈)
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
탐욕 알고리즘의 가장 대표적인 문제로 거스름돈 문제가 있습니다. 가장 최소 갯수로 동전을 거슬러주는 문제입니다.
package test;
public class 거스름돈 {
public static void main(String[] args) {
int money = 800;
int c500 = money / 500;
money -= c500 * 500;
int c400 = money / 400;
money -= c400 * 400;
int c100 = money / 100;
money -= c100 * 100;
int c50 = money / 50;
money -= c50 * 50;
int c10 = money / 10;
money -= c10 * 10;
System.out.printf("500원: %d\n", c500);
System.out.printf("100원: %d\n", c100);
System.out.printf(" 50원: %d\n", c50);
System.out.printf(" 10원: %d\n", c10);
}
}만약 돈을 800원 들고 있고, (500, 400, 100, 50, 10원) 단위로 거슬러 줄 수 있다면, 정답은 500원 1개, 100원 3개가 나올 것입니다.
이처럼 400원짜리가 있어도 400원 2개를 거슬러주는 게 최적인데, 탐욕은 작동하지 않는 것을 확인할 수 있습니다.
즉, 지역적으로 최적의 선택이 최종의 최적선택이 아닐 수 있다는 의미입니다.
3. 패턴 매칭 (고지식한 패턴 검색 알고리즘)
package test;
public class 패턴매칭 {
public static void main(String[] args) {
char[] t = "This iss a book".toCharArray(); //string -> char[]
char[] p ="iss".toCharArray();
int idx = pattern(p,t);
}
private static int pattern(char[] p, char[] t) {
int n=t.length;
int m = p.length;
for(int i=0;i<n-m+1;i++) {
//pattern이 한 칸씩 shift가 최대 n-m+1번 수행
boolean flag = true;
for(int j=0;j<m;j++) {
//각 shift에서 1:1비교가 최대 m번 수행
if(p[j]!=t[i+j]) {//일치하지 않는게 발견되면
flag = false;//일치하지 않는다고 바꾼다
break;
}//다 돌았을 때 flag => true : 모두 일치
//flag => false : 모두 일치 X
if(flag) return i;
}
return -1;
}
return 0;
}
}
4. 부분 집합
공집합일 때 부터 1,2,3의 조합이 모두 들어갈 때 까지 즉, 집합이 0개일 때부터 1개일 때 2개일 때... 전체 다 들어갔을 때를 따져줍니다.
package arr;
import java.util.Scanner;
/**
* 부분집합
*
*
* */
public class PowerSet {
static int[] arr = {1,2,3};
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
sel=new int[N];
powerset(0);
}
static public void powerset(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
if(sel[i]!=0)System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
sel[depth]=arr[depth];
powerset(depth+1);
sel[depth]=0;
powerset(depth+1);
}
}
[결과]

3 밑에 공집합인 경우인 공백도 나옵니다.
결과를 보면, 부분집합(power set)은 순서를 중요하게 생각하지 않는 것을 알 수 있습니다.
즉, (1,2)와 (2,1)은 같은 것으로 보고 결과로 도출되지 않습니다.
5. 조합
조합은 부분 집합에서 집합의 갯수를 정해놓은 셈입니다.
package arr;
import java.util.Scanner;
/**
* 조합
*
*
* */
public class Combination {
static int[] arr = {1,2,3};
static int[] sel;
static int N,C;
public static void main(String[] args) {
N = 3;
C=2;
sel=new int[C];
powerset(0,0);
}
static public void powerset(int depth, int idx) {
if(depth==C) {
for(int i=0;i<C;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
if(idx == N) return;
sel[depth]=arr[idx];
powerset(depth+1,idx+1);//idx를 넘겨주면 중복 조합
sel[depth]=0;
powerset(depth,idx+1);
}
}
[결과]

결과를 보면 부분집합에서 2가지를 고려한 경우만 답으로 나오는 것을 확인할 수 있습니다.
즉, 전체 경우의 수를 고려해야 할 때는 부분 집합, 특정한 갯수를 꼭 채워서 고려해야한다면 조합을 사용해야 합니다.
6. 순열
부분집합은 조합과는 다르게 순서를 중요하게 생각합니다. 즉, (1,2)와 (2,1)은 다른 것으로 보고 결과로 도출합니다.
package arr;
import java.util.Scanner;
/**
* 순열
* 순서 전체를 돌려줘야함
* 선택된 곳은 가면 안됨 -> 같은 숫자가 나오는 경우는 없음
* */
public class Permutation {
static int[] arr = {1,2,3};
static boolean[] visited;
static int[] sel;
static int N;
public static void main(String[] args) {
N = 3;
visited = new boolean[N];
sel=new int[N];
permutation(0);
}
static public void permutation(int depth) {
if(depth==N) {
for(int i=0;i<N;i++) {
System.out.print(sel[i]+" ");
}
System.out.println();
return;
}
for(int i=0;i<N;i++) {
if(visited[i]) continue;
sel[depth]=arr[i];
visited[i]=true;
permutation(depth+1);
visited[i]=false;
}
}
}
[결과]
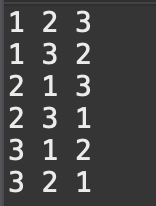
7. DFS/BFS

DFS는 깊이 우선 탐색 방식입니다. 4방 탐색 후 갈 수 있는 곳으로 재귀를 불러 시스템 스택을 쌓습니다.
반면 BFS는 큐를 이용하는 것이 대표적입니다. 다음과 같은 과정을 거칩니다.
- 출발지점을 queue에 집어넣고, 방문처리한다.(출발지점을 구지 넣는 이유는 q가 첫 시작부터 비면 안되기 때문이다.)
- 4방 탐색하면서 갈 수 있는 경로 모두를 queue에 넣고 방문처리한다.
- 이 작업을 queue가 빌 때까지 계속한다.
- queue가 빈다는 것은 더이상 갈 수 있는 경로가 없다는 것을 의미한다.
예시 문제 ) 미로 1 (1226. [S/W 문제해결 기본] 7일차 - 미로1)
/**
* DFS는 4방 탐색 후 갈 수 있는 곳으로 재귀를 불러 시스템 스택을 쌓는다.
* */
public static void DFS(int startR, int startC) {
//상 하 좌 우
int[][] drc = {{-1,0},{1,0},{0,-1},{0,1}};
for(int direc=0;direc<4;direc++) {
int row = startR+drc[direc][0];
int col = startC+drc[direc][1];
//경계체크
if(row<0 || row>=16 || col<0 || col>=16) continue;
//case 1. 벽을 만나면 다른 경로 찾기
if(map[row][col]==1) continue;//벽을 만나도 전체 미로 찾기를 종료하면 안됨 다른 경로를 찾아야 한다.
//case 2. 탈출구를 만나면 return
if(map[row][col]==3) {
flag=true;//탈출가능
return;
}
//case 3. 통로를 만나면 시스템 스택 쌓기
//방문을 체크해주는 이유 인접한 다음 위치에서 4방탐색하며 방문했던 현재 위치를 또 방문할 수 있기 떄문이다.
if(!visited[row][col] && map[row][col]==0) {
visited[row][col]=true;
DFS(row,col);//이 row, col에서 새로운 시작
}
}
}
/**
* 출발지점을 queue에 집어넣고, 방문처리한다.(출발지점을 구지 넣는 이유는 q가 첫 시작부터 비면 안되기 때문이다.)
* 4방 탐색하면서 갈 수 있는 경로 모두를 queue에 넣고 방문처리한다.
* 이 작업을 queue가 빌 때까지 계속한다.
* queue가 빈다는 것은 더이상 갈 수 있는 경로가 없다는 것을 의미한다.
* */
static public void BFS(int startR, int startC) {
//상 하 좌 우
int[][] drc= {{-1,0},{1,0},{0,-1},{0,1}};
Queue<node> queue = new LinkedList<>();
node startNode = new node(startR, startC);
queue.offer(startNode);
while(!queue.isEmpty()) {
//현재 시작할 노드를 뽑기
node curr = queue.poll();
//4방탐색
for(int i=0;i<4;i++) {
int row = curr.r+drc[i][0];
int col = curr.c+drc[i][1];
//경계체크
if(row<0 || row>=100 || col<0 || col>=100) continue;
//벽 만났으면
if(map[row][col]==1) continue;
//탈출구를 만나면 flag를 true로 바꿔라
if(map[row][col]==3) {
flag=true;
return;
}
//갈 수 있는 길을 만나면 queue에 추가
if(!visited[row][col] && map[row][col]==0) {
node newNode = new node(row,col);
queue.offer(newNode);
visited[row][col]=true;
}
}//4방 탐색 끝
}
}
8. APS (크루스칼)
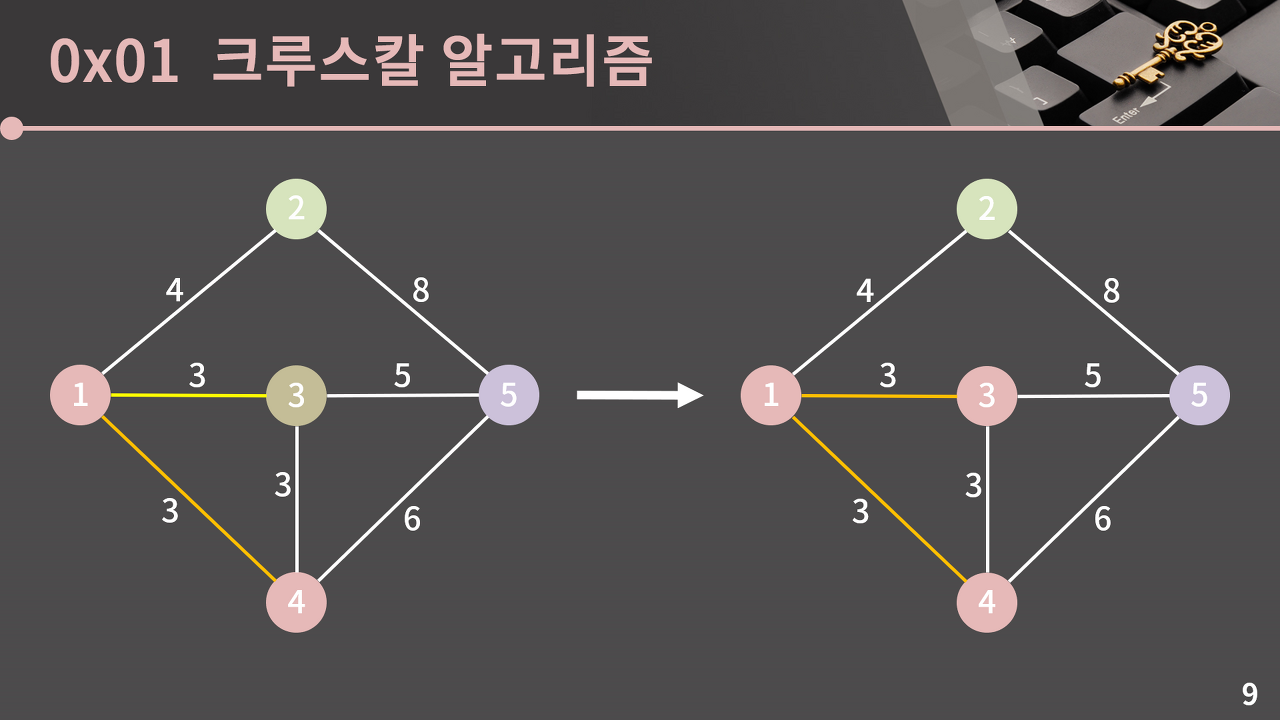
그리디 알고리즘 중에 하나인 크루스칼 알고리즘입니다. 간선을 하나씩 선택해서 MST(최소 스패닝 트리)를 찾는 알고리즘입니다.
크루스칼은 가장 먼저 간선의 가중치에 따라서 정렬을 해줘야 합니다.
또한 두 노드가 같은 부모를 가지면 사이클이 발생합니다. 때문에 서로 다른 부모를 가진 노드만 연결될 수 있습니다.
package daily0329;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;
public class 크루스칼 {
// 크루스칼 알고리즘
// Union-Find 알고리즘
static int[] p;// 부모를 저장할 배열
static node[] nodes; // 노드들을 기록한 배열
static class node {
int startNode;
int endNode;
int score;
node(int startNode, int endNode, int score) {
this.startNode = startNode;
this.endNode = endNode;
this.score = score;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());//test case
for(int T=1;T<t+1;T++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken()); // 정점의 개수
int E = Integer.parseInt(st.nextToken()); // 간선의 개수
nodes = new node[E]; //nodes는 0부터 시작
// 간선으로 연결된 정점들의 정보를 받는다.
// 차례대로 시작노드, 끝노드, 가중치
//nodes는 0부터 시작
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
node newNode = new node(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
nodes[i] = newNode;
}
// 간선을 정렬합니다. -> 가중치 순으로 정렬합니다 -> 오름차순
Arrays.sort(nodes, new Comparator<node>() {
@Override
public int compare(node o1, node o2) {
return o1.score - o2.score;
}
});
// 간선을 선택하자! -> 사이클이 발생 안하는 친구들로만 뽑자.
// 사이클이 발생한다는 것은 찐 부모가 같을 때이다.
// 일단 부모를 초기화 하자 -> 먼저 내가 부모가 되는 것이다.
p = new int[V+1];//정점들이 1번부터 시작함
for (int i = 1; i <= V; i++) {
makeSet(i);
}
// 내가 가중치가 가장 적은 간선을 하나 뽑아서 그 간선의 시작노드와 끝노드의 부모가 같은지 확인해줄것이다.
// 간선은 v-1개를 뽑아야 최소로 연결된다.
int pick = 0; // v-1개 뽑자
long fee = 0; // 최소 비용은 얼마일까 : 가중치 값이 1,000,000이 누적되면 int 범위 넘으므로, result를 long 타입
StringBuilder sb = new StringBuilder();
// E만큼의 정점을 하나씩 선택하는 과정을 거친다.
//nodes는 0부터 시작
for (int i = 0; i < E; i++) {
// 시작점과 끝점의 부모를 찾는다.
int node1 = findSet(nodes[i].startNode);
int node2 = findSet(nodes[i].endNode);
// 부모가 다르면 간선으로 채택 가능하며, 서로 연결해줄 수 있다.
if (node1 != node2) {
union(node1, node2);
pick++;
fee += nodes[i].score;
}
if (pick == V - 1)
break;
}
sb.append("#").append(T).append(" ").append(fee);
System.out.println(sb);
}//test case end
}
static public void makeSet(int num) {
p[num] = num; // num의 부모는 num이다.
}
// 엄마를 찾아줘
static public int findSet(int num) {
// 부모를 찾았더니 나라면? 나를 반환
if (p[num] == num)
return num;
// 근데 내가 부모가 아니다 -> 다른 부모가 있다는 것이다 -> 재귀타고 찐부모를 찾아줘
return p[num]=findSet(p[num]);//찾는 것에서 끝나지 말고 저장까지 해준다.
}
// 노드를 연결한다는 것은 부모를 바꾼다는 뜻이다.
// 지금은 p에 자기 자신을 부모로 뒀지만, 간선을 채택함으로써 작은쪽이 큰쪽으로 들어간다.
static public void union(int node1, int node2) {
// node2 찐부모의 값에 node1의 찐부모를 넣어주겠다.
p[findSet(node2)] = findSet(node1);
}
}
9. 다익스트라
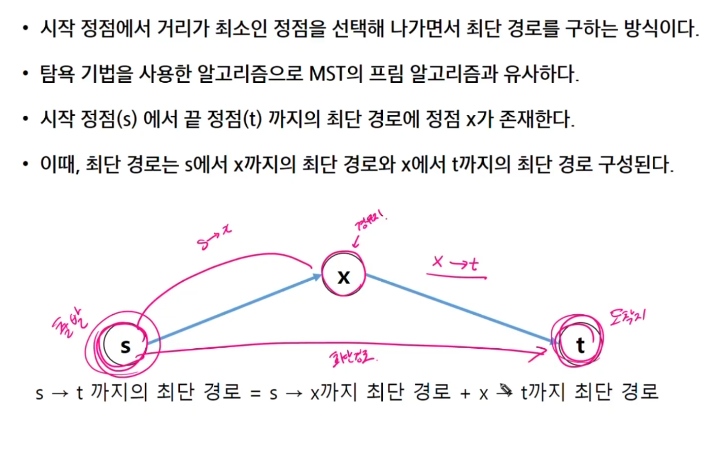
다익스트라 알고리즘은 시작 정점에서 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식입니다. 때문에 다익스트라 알고리즘은 시작 정점이 중요합니다.
하나의 시작 정점에서 끝 정점까지의 최단 경로를 구하는 방식은 2가지입니다. 그 중 다익스트라는 음의 가중치를 허용하지 않고, 벨만 포드는 음의 가중치는 허용합니다.
package test;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class 다익스트라알고리즘 {
static class Node implements Comparable<Node> {
int v, w;
public Node(int v, int w) {
this.v = v;
this.w = w;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.w, o.w);
}
}
static final int INF = Integer.MAX_VALUE;
static int V, E; // V : 정점 , E: 간선
static List<Node>[] adjList; // 인접리스트
static int[] dist; // 최단 길이를 저장할 배열
public static void main(String[] args) {
Scanner sc = new Scanner(input);
V = sc.nextInt();
E = sc.nextInt();
adjList = new ArrayList[V];
for (int i = 0; i < V; i++)
adjList[i] = new ArrayList<>();
dist = new int[V];
Arrays.fill(dist, INF);
// 입력 받기
for (int i = 0; i < E; i++) {
int A = sc.nextInt();
int B = sc.nextInt();
int W = sc.nextInt();
// 유향 그래프였다.
adjList[A].add(new Node(B, W)); // 인접리스트 노드 추가
// 아래의 한줄 코드가 위의 4줄을 커버하지만 익숙치 않은 상황이라면 자제할것
// adjList[sc.nextInt()].add(new Node(sc.nextInt(), sc.nextInt()));
}
dijkstra(0);
//System.out.println(Arrays.toString(dist));
}
private static void dijkstra(int start) {
// 우선순위 큐를 이용해서 집어 넣을 때 그냥 때려넣지 말고
// 갱신한 값을 만들어서 새로운 노드를 집어넣어라.
boolean[] visited = new boolean[V];
Queue<Node> pq = new PriorityQueue<>();
dist[start] = 0;
pq.offer(new Node(start, 0));// 첫값을 넣어준다.
while (!pq.isEmpty()) {
int now = pq.poll().v;// 현재 고려중인 이동지
if (!visited[now]) {
visited[now] = true; // 현재 이동지를 갔다고 말해주기
for (Node next : adjList[now]) {
if (dist[next.v] > dist[now] + next.w) {
dist[next.v] = dist[now] + next.w;
pq.offer(new Node(next.v, dist[next.v]));
}
}
}
}
// 최소거리 출력
for (int i : dist) {
if (i == INF)
System.out.print(0 + " ");
else
System.out.print(i + " ");
}
}
static String input = "6 11\r\n" + "0 1 4\r\n" + "0 2 2\r\n" + "0 5 25\r\n" + "1 3 8\r\n" + "1 4 7\r\n"
+ "2 1 1\r\n" + "2 4 4\r\n" + "3 0 3\r\n" + "3 5 6\r\n" + "4 3 5\r\n" + "4 5 12\r\n" + "";
}[출력] 0 3 2 11 6 17
10. 위상정렬
순서가 있는 작업을 차례로 진행해야 할 때 순서를 결정해 주기 위해 사용하는 알고리즘이 위상정렬입니다.
사이클이 없는 방향 그래프(Directed Acyclic Grape, DAG)의 모든 노드를 주어진 방향성에 어긋나지 않게 순서를 나열하는 것입니다. 즉, 정답은 여러가지가 존재할 수 있다는 의미입니다.
위상정렬의 특징은 다음과 같습니다.
1) 모든 정점을 방문하기 전에 큐가 공백상태가 되면 사이클이 존재하는 것이다.
2) 그래프 유형은 DAG여야 한다.
3) 여러 해답이 존재할 수 있다. 그 이유는 진입 차수가 0인 값이 동시에 생성된다면 작성한 코드 방법에 따라 답이 달라지기 때문이다.
4) 시간 복잡도는 O(V+E), 간선+정점의 시간복잡도이다.
예시 문제 ) 줄 세우기 (2252. 줄 세우기)
2252번: 줄 세우기
첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의
www.acmicpc.net
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static List<Student>[] stList;
static int[] result;
static int N;
static int[] in;//내가 일을 처리하기 위해 거쳐야할 학생 수
static class Student{
int StudentNo;
public Student(int StudentNo) {
super();
this.StudentNo = StudentNo;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt(); //학생의 수
int M = sc.nextInt(); //키 비교 횟수
in = new int[N+1];
//학생들의 키정보를 저장할 list
stList = new ArrayList[N+1];//1번 학생부터 시작
for(int i=0;i<N+1;i++) {
stList[i]=new ArrayList<>();
}
//학생들 키 비교 입력받기
for(int i=0;i<M;i++) {
int A = sc.nextInt();
int B = sc.nextInt();
//A학생 뒤에 서는 B를 추가
stList[A].add(new Student(B));
in[B]++;//내 앞에 한 명 추가
}
//구현
result = new int[N];
StudentOrder();
//결과출력
for(int i=0;i<N;i++) {
System.out.print(result[i]+" ");
}
System.out.println();
}
/**
* 1) 나보다 큰 사람이 없으면 즉, in이 0인 곳을 큐에 추가해준다.
* 2) 하나를 꺼내서 그 사람 뒤에오는 사람들 -1을 해준다.
* 3) 왜냐하면 지금 꺼낸 애 결과로 반영되었기 때문이다.
* */
public static void StudentOrder() {
Queue<Integer> q = new LinkedList<>();
int idx=0;//결과 인덱스
for(int i=1;i<=N;i++) {
if(in[i]==0) q.add(i);
}
while(!q.isEmpty()) {
int curr = q.poll();
result[idx++]=curr;
for(int i=0;i<stList[curr].size();i++) {
int next = stList[curr].get(i).StudentNo;
in[next]--;
if(in[next]==0)q.add(next);
}
}
}
}
사실 알고리즘은 꾸준히 풀어보고 감을 익혀야하는 학문 같아요!
기본 알고리즘의 이해가 훌륭하시다면, 1일 1알고리즘 도전해보시는 것이 어떨까요?
보시면서 오류가 있다면 댓글로 남겨주세요!
'대외활동 > SSAFYicial' 카테고리의 다른 글
| [CS 정리는 내가 할게, 면접은 누가볼래? - 프론트엔드/RN편] 프론트엔드/React Native 면접 질문 필수 암기 모음집 2탄 (1) | 2023.10.23 |
|---|---|
| [회고] 내가 만약 특화프로젝트 1일차로 돌아간다면? 하반기 취준과의 전쟁 (0) | 2023.10.22 |
| [TMI] 신한 해커톤 with SSAFY 현장 속으로! (0) | 2023.09.26 |
| [CS 정리는 내가 할게, 면접은 누가볼래? - 프론트엔드/React편] 프론트엔드/React 면접 질문 필수 암기 모음집 1탄 (2) | 2023.08.26 |
| [회고] 내가 만약 공통프로젝트 1일차로 돌아간다면? 공통프로젝트를 마치며 깨달은 것들 (7) | 2023.08.20 |

