포워딩하기 위해선 포워딩 테이블이 필요합니다. 포워딩 테이블을 생성하는 역할을 하는 것은 control plane입니다. 제어하는 정보들이 오고다니는 부서이죠.
1. 라우팅 알고리즘
네비게이션에서 목적지를 지정하고 가는 경로는 추천받는데, 네비게이션마다 추천 경로가 다를 수 있습니다. 네트워크에서도 마찬가지 입니다. 트래픽을 소스에서 목적지까지 구할 겁니다. 네트워크 사업장마다 라우팅하는 목적은 조금씩 다를 수 있습니다. 속도, 요금, congestion 매트릭을 규정하기 나름입니다.
1-1. 라우팅 알고리즘의 목적
source 라우터에서 목적지 라우터까지 좋은 길(good path)을 찾는 겁니다. good path란 어떤 비용을 최소화해주는 거리를 말합니다. 비용은 사업자들마다 정의하는 기준(거리, 시간, 돈 혹은 여러가지의 조합 등)이 다릅니다.
default router(디폴트 라우터) : 호스트(소스 혹은 목적지)를 기준으로해서 1hop에 있는 라우터를 의미합니다.
이 디폴트 라우터는 2가지로 분기될 수 있습니다.
1) 소스쪽에 붙어있는 라우터인 소스라우터
2) destination에 붙어있는 라우터인 destination 라우터
1-2. 그래프 abstraction
좋은 길을 찾기 위해선 네트워크 토폴로지를 abstraction할 필요가 있습니다.
그래프 이론을 표현하는 방법을 이해해보는 시간을 갖도록 하겠습니다.
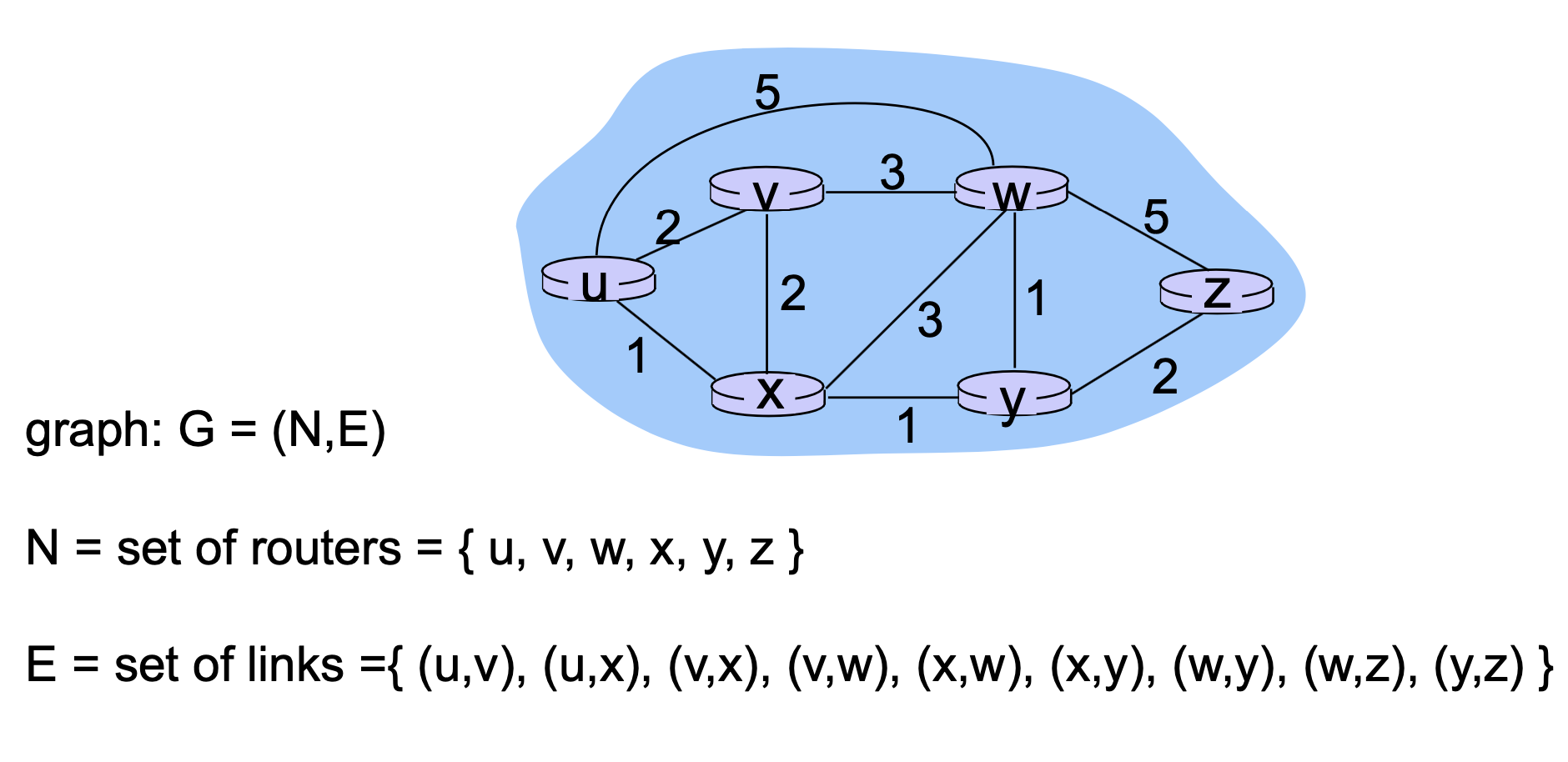
다음과 같은 네트워크 토폴로지는 edge라고 하는 노드로 구성이 되어있습니다. 노드들은 링크들로 연결이 되어 있어요. 이것을 수학적으로 표현하면, 노드(라우터)들의 set이 다음과 같이 표현이 될 수 있습니다.
그래프는 아래 2줄 N,E를 포함한다는 뜻으로 G(그래프)를 설정하는 것으로 시작합니다.
u, v, w, x, y, z 이렇게 6개의 노드가 있습니다.
또한 이 노드들이 연결되는 링크를 정의할 수 있겠습니다. 링크 (u, v), (u, x) 등의 순서쌍으로 정의가 됩니다. 연결되지 않은 링크는 들어가있지 않을 겁니다.
이렇게 비쥬얼라이즈된 수학을 단 2줄의 식으로 표현하는 것이 그래프 이론입니다.
그래프 이론은 노드(라우터)와 링크의 set으로 표현이 될 수 있습니다.
1-3. 그래프 abstraction : 비용 정의
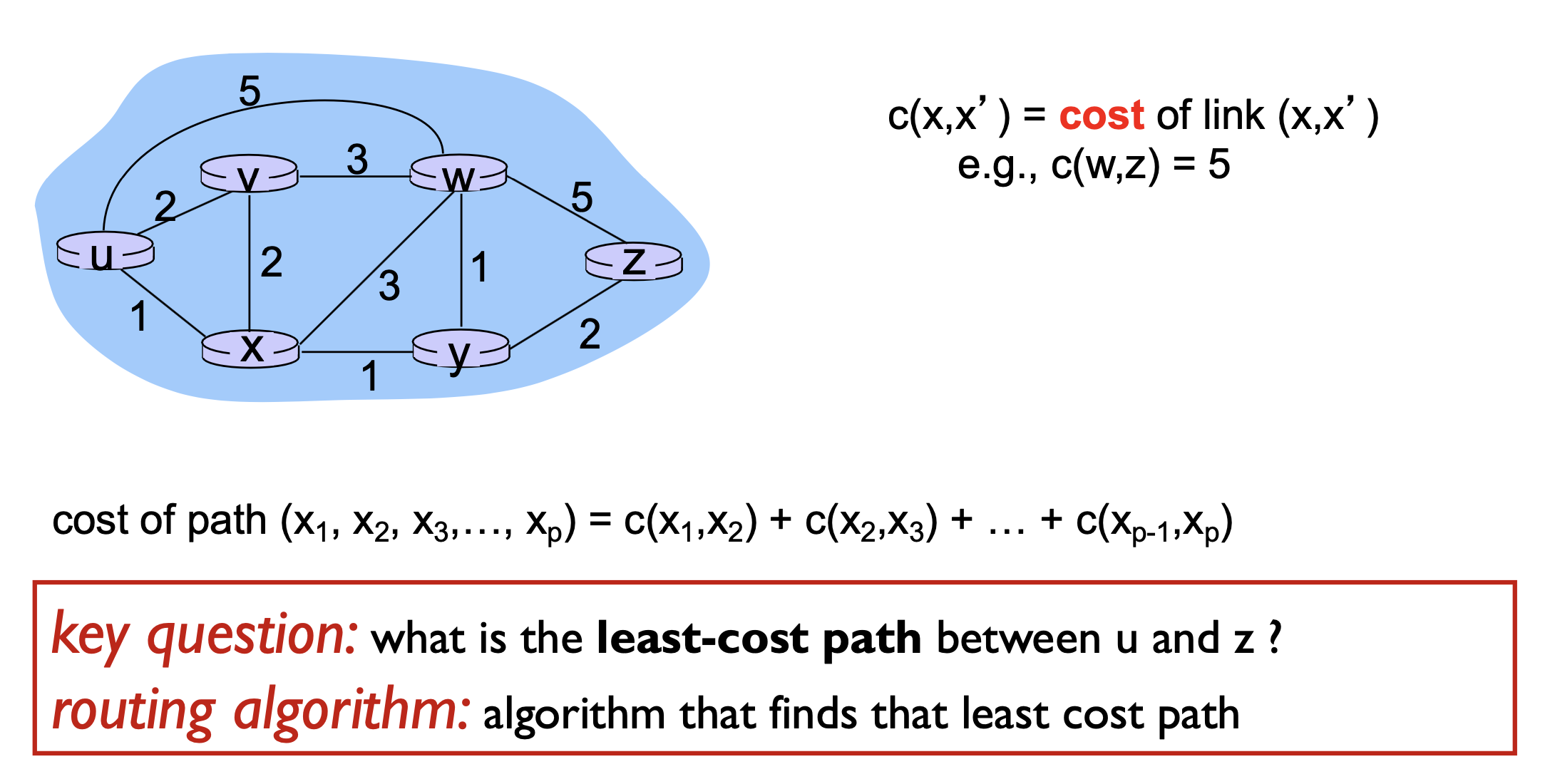
링크 x와 x' 즉, 어떤 링크 사이에서 발생하는 비용을 C라고 정의해봅시다.
모든 링크에서 발생하는 cost의 합은 다음과 같이 (x1, x2, ... , xp) = C(x1, x2) + C(x2, x3)...+C(x(p-1),xp)라고 표현할 수 있습니다.
그렇다면 어떤 알고리즘을 적용해야 최소 비용이 발생하는 경로를 알아낼 수 있을까요?
여러 경로 중 least cost path는 어디이고, 최소 비용을 구하는 라우팅 알고리즘은 무엇인지 찾는 것 입니다.
이런 경우 2가지 information을 통해 해결할 수 있는데요.
1) global information

산 전체에 대한 토폴로지를 알고, 어떤 경로로 가야 제일 빨리 가는지 먼저 계산한 다음에 그 경로를 따라가는 것 입니다.
2) decentralized information

그 때 그 때 가다보면 돌아갈 순 있겠지만, 정상을 향해 가게 되어있습니다. 갈 때 마다 표지판이 있으니까요. 이런 케이스는 전체 산 모습이 어떻게 되어있는지는 일단 모릅니다.
위의 2가지 information 가운데 global information이 더 빠르게 최적의 길을 구축할 수 있겠죠? 실제 알고리즘에서도 그럽니다. 현재 많이 쓰이기도 하죠.
하지만 단점이 있습니다.
1) 연산량이 많기 때문에 전체 라우팅 path에 적용하는 것은 무리가 있습니다. 구역단위로 쪼개서 적용해요.
2) global information이 존재한다는 가정이 있다는 건데, 네트워크 토폴로지는 일정할지 몰라도 cost는 계속 변할 수 있습니다. 계속 실시간 업데이트를 해줘야한다는 뜻입니다. global information을 만들기 위한 cost가 필요하다는 뜻입니다.
이런 이유로 만들기가 쉽고 (주변 정보만 모으기 때문) 정보 획득 비용이 적고, 연산량도 적은 decentralized information을 사용하기도 합니다.
역시 단점도 있죠.
최적의 경로를 보장하지 못하고, 반복해서 실행하다 보면 최적으로 수렴하지만 시간이 너무 오래걸립니다.
최적의 경로가 목적이 아닌 적당히 반복해서 실행하다 보면 최적으로 수렴한다는 원리로 점진적으로 개선한다는 방향을 두고서 적용하는 알고리즘 입니다.
라우팅 알고리즘에서도 2가지 approach(distance알고리즘과 백터 알고리즘)가 있다고 했는데, 각각 어떤 정보를 활용하느냐에 따라서 갈리게 됩니다.
여기서 global information은 link state 알고리즘과 같습니다.
decentralized information은 distance vetor 알고리즘과 같습니다.
2. link state 알고리즘의 구현
두 알고리즘 모두 각각의 라우터는 자기 이웃의 정보는 알고 있어야합니다.
라우팅 프로토콜을 통해서 이웃정보를 모으는 것(gathering)을 지원합니다.
이웃 라우터까지 링크 비용은 얼마인지까지 알려줍니다. 2hop까지 떨어지는 이웃부터는 모릅니다. 자신이 알아내야하는 정보이죠.
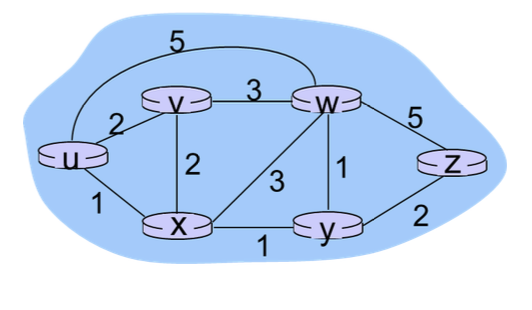
위의 그림에서 z는 아래는 알지만, 다른 이웃은 모를겁니다.
w->z : cost 5
y->z : cost 2
global information 즉, link state 알고리즘은 전체 토폴로지와 전체 링크의 비용을 알고 있어야한다고 했습니다.
근데, 나의 이웃만 아는 상태에서 어떻게 각각의 라우터는 전체 뷰를 얻을 수 있는걸까요?

자신이 가지고 있는 이웃정보를 전체 네트워크로 floods 시킵니다. 전체 정보를 얻은 다음에야 각각의 라우터들은 shotest path를 계산하게 되는 것입니다.

하지만 이런 방식을 쓰면 안좋은 점이 있습니다. 트래픽이 너무 많이 들어간다는 점이에요. link state의 단점이자 비용입니다.
flooding을 하며 너무 많은 오버헤드가 발생합니다. 전세계 단위로는 못하고, 구역 단위로 알고리즘이 돌아갈 겁니다.
다익스트라 알고리즘은 link state 알고리즘에서 사용됩니다. 위의 상태에서 어떤 식으로 다익스트라 알고리즘이 사용될까요?
2-1. 다익스트라 알고리즘
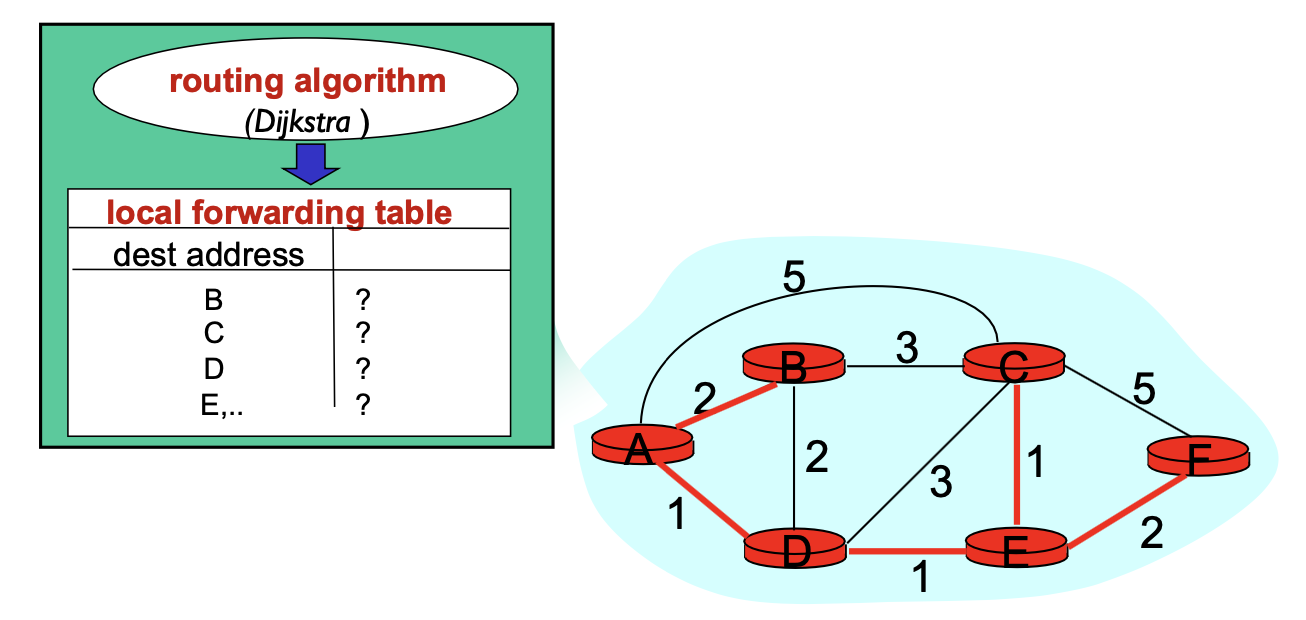
다익스트라 알고리즘은 각각의 노드에서 돌아갑니다. 그러면 각각의 라우터는 forwading 테이블을 얻고 테이블에는 최소 비용 path입니다. 최소 비용 path는 자기를 제외한 모든 라우터들에 대한 최소 경로 포트가 나오는 겁니다.
다익스트라 알고리즘의 INPUT : 네트워크 토폴로지와 링크 cost
다익스트라 알고리즘의 OUTPUT : 자신을 제외한 모든 경로의 최소 비용 경로(포워딩 테이블)
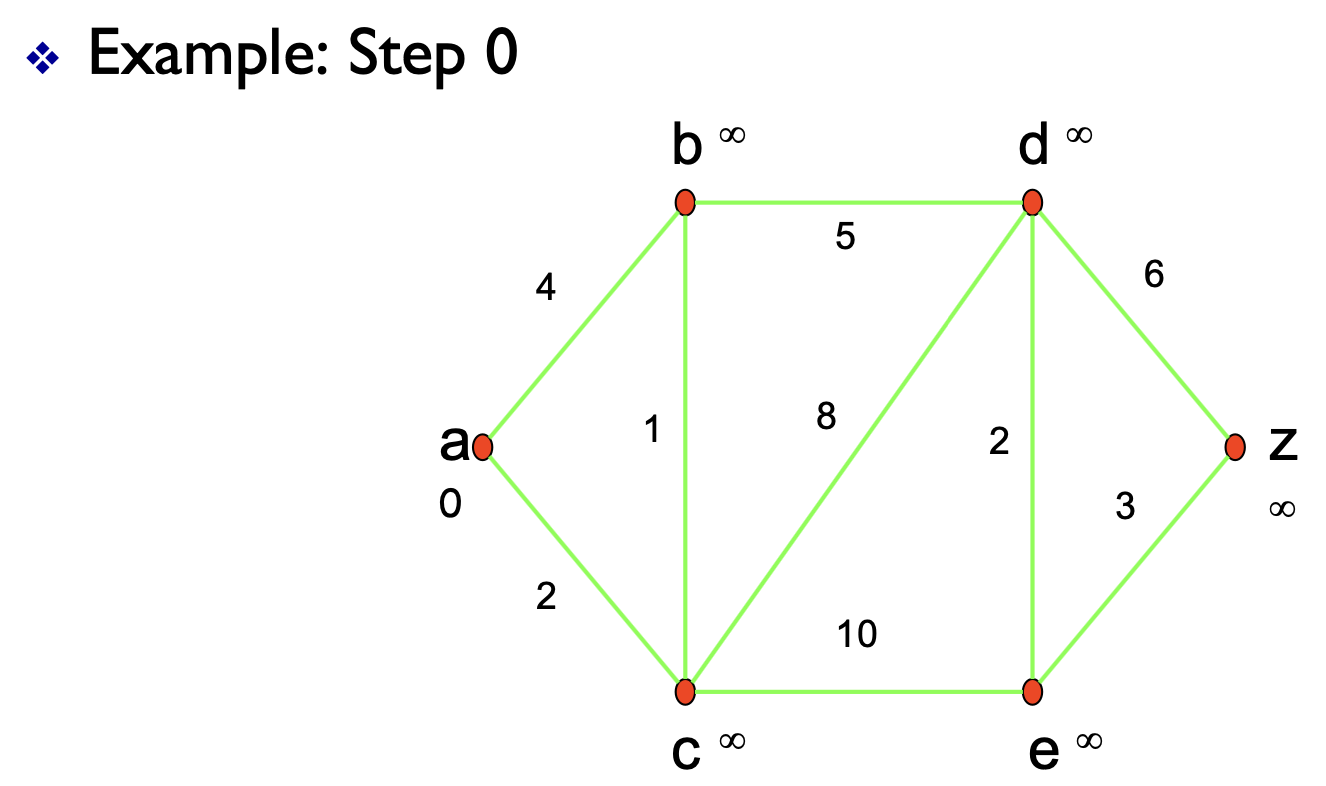
첫 지점을 제외한 나머지 구간을 무한대로 설정합니다. 제일 작은 cost가 출발점으로 설정되는 것입니다.


'CS > 컴퓨터 네트워크' 카테고리의 다른 글
| 컴퓨터 네트워크컴퓨터 네트워크 23일차 : (0) | 2021.11.30 |
|---|---|
| 컴퓨터 네트워크컴퓨터 네트워크 21일차 : Distance Vector 알고리즘(2) (0) | 2021.11.17 |
| 컴퓨터 네트워크 19일차 : 라우터 기능, 방화벽 (0) | 2021.11.09 |
| 컴퓨터 네트워크 18일차 : IP addressing, DHCP, NAT (0) | 2021.11.06 |
| 컴퓨터 네트워크 17일차 : Network layer (0) | 2021.11.03 |
